Perpangkatan dengan Segitiga Pascal

Untuk menguraikan bentuk aljabar (a+b)² kamu dapat menyelesaikannya dalam waktu singkat. Akan tetapi, bagaimana dengan bentuk aljabar (a+b)³, (a+b)⁴, (a+b)⁵, dan seterusnya? Tentu saja kamu juga dapat menguraikannya, meskipun akan memerlukan waktu yang lebih lama. Untuk memudahkan penguraian perpangkatan bentuk-bentuk aljabar tersebut, kamu bisa menggunakan pola segitiga Pascal.
Sekarang, perhatikan pola segitiga Pascal berikut.

Hubungan antara segitiga Pascal dengan perpangkatan suku dua bentuk aljabar adalah sebagai berikut.

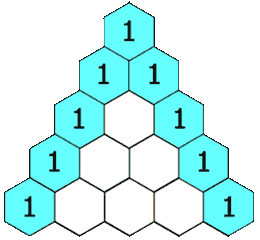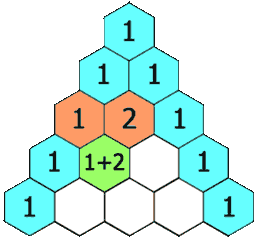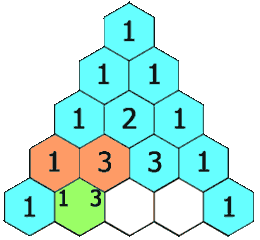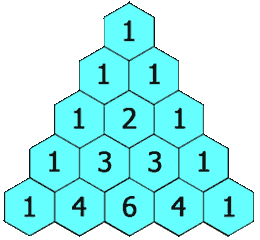
Sebelumnya, kamu telah mengetahui bahwa bentuk aljabar (a + b)² dapat diuraikan menjadi a² + 2ab + b². Jika koefisien-koefisiennya dibandingkan dengan baris ketiga pola segitiga Pascal, hasilnya pasti sama, yaitu 1, 2, 1. Ini berarti, bentuk aljabar (a + b)² mengikuti pola segitiga Pascal. Sekarang, perhatikan variabel pada bentuk a² + 2ab + b². Semakin ke kanan, pangkat a semakin berkurang (a² kemudian a). Sebaliknya, semakin ke kanan pangkat b semakin bertambah (b kemudian b²). Jadi, dengan menggunakan pola segitiga Pascal dan aturan perpangkatan variabel, bentuk-bentuk perpangkatan suku dua (a + b)³, (a + b)⁴, (a + b)⁵, dan seterusnya dapat diuraikan sebagai berikut.

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

dan seterusnya.

Contoh Soal

a. (x + 5)³

b. (2x + 3)³

c. (x – 2)⁴

d. (3x – 4)³

e. (4x + 5y)³

f. (2x + 3y)³

g. (3x – 2y)⁴

h. (3x – 4y)³

Jawab:

a. (x + 5)³ misal a = x dan b = 5 maka,

(a + b)³ = a³ + 3a²b + 3ab² + b³, substitusi a = x dan b = 5 maka,

(x + 5)³ = x³ + 3x²5 + 3x5² + 5³

(x + 5)³ = x³ + 15x² + 75x + 125

b. (2x + 3)³ misal a = 2x dan b = 3 maka

(a + b)³ = a³ + 3a²b + 3ab² + b³, substitusi a = 2x dan b = 3 maka,

(2x + 3)³ = (2x)³ + 3(2x)²3 + 3(2x)3² + 3³

(2x + 3)³ = 8x³ + 36x² + 54x + 27

c. (x – 2)⁴ misal a = x dan b = -2 maka

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ substitusi a = x dan b = -2 maka,

(x – 2)⁴ = x⁴ + 4x³(-2) + 6x²(-2)² + 4x(-2)³ + (-2)⁴

(x – 2)⁴ = x⁴ - 8x³ + 24x² - 32x + 16

d. (3x – 4)³ misal a = 3x dan b = -4 maka

(a + b)³ = a³ + 3a²b + 3ab² + b³, substitusi a = 3x dan b = -4 maka,

(3x – 4)³ = (3x)³ + 3(3x)²(-4) + 3(3x)(-4)² + (-4)³

(3x – 4)³ = 27x³ - 108x² + 144x - 64

e. (4x + 5y)³ misal a = 4x dan b = 5y maka

(a + b)³ = a³ + 3a²b + 3ab² + b³, substitusi a = 4x dan b = 5y maka,

(4x + 5y)³ = (4x)³ + 3(4x)²(5y) + 3(4x)(5y)² + (5y)³

(4x + 5y b)³ = 64x³ + 240x²y + 300xy² + 125y³

f. (2x + 3y)³ misal a = 2x dan b = 3y maka

(a + b)³ = a³ + 3a²b + 3ab² + b³, substitusi a = 2x dan b = 3y maka,

(2x + 3y)³ = (2x)³ + 3(2x)²(3y) + 3(2x)(3y)² + (3y)³

(2x + 3y)³ = 8x³ + 36x²y + 54xy² + 27y³

g. (3x – 2y)⁴ misal a = 3x dan b = -2y maka

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ substitusi a = 3x dan b = -2y maka,

(3x – 2y)⁴ = (3x)⁴ + 4(3x)³(-2y) + 6(3x)²(-2y)² + 4(3x)(-2y)³ + (-2y)⁴

(3x – 2y)⁴ = 81x⁴ - 216x³y + 216x²y² + 96xy³ + 16y⁴

h. (3x – 4y)³ misal a = 3x dan b = -4y maka

(a + b)³ = a³ + 3a²b + 3ab² + b³, substitusi a = 3x dan b = -4y maka,

(3x – 4y)³ = (3x)³ + 3(3x)²(-4y) + 3(3x)(-4y)² + (-4y)³

(3x – 4y)³ = 27x³ - 108x²y + 144xy² + 256y³

Demikian tips cara mengerjakan soal perpangkatan dalam bentuk aljabar. Dari penjelasan dan contoh soal di atas maka dapat disimpulkan tips cara mengerjakan soal dalam bentuk aljabar sebagai berikut.

1.            Gunakan segitiga pascal untuk menentukan hasil dari (a + b)ⁿ

2.            Gunakan permisalan untuk memudahkan dalam pengerjakan soal-soal tersebut

3.            Substitusikan permisalan tadi ke hasil yang diperoleh dalam segitiga Pascal. Silahkan lihat contoh soalnya.

Sumber : http://mafia.mafiaol.com/2013/09/tips-mengerjakan-soal-perpangkatan.html